Cet article est entièrement extrait d’un recueil de note de Claude E. Shannon: aux éditions Collected Papers : N. J. A. Sloane; Aaron D. Wyner.
Nom original : Scientific Aspects of Juggling, publié en 1993.
Je l’ai traduit en partie à l’aide d’outils de traduction en ligne. Néanmoins, je l’ai corrigé pour que ça soit au moins compréhensible. Si une machine pouvait tout faire, ça serait franchement inquiétant. Néanmoins, je tiens à informer le lecteur averti d’expérimenter tout ce qui est inscrit dans cet article. Cette discipline à beaucoup évolué en trois décennies, certains records évoqués ici ne sont plus d’actualité…
»Pensez-vous que la jonglerie est un simple tour? » demanda le petit homme, l’air blessé. « Un amusement pour les guetteurs ? Un moyen de ramasser une couronne ou deux à un carnaval de province ? C’est toutes ces choses, oui, mais c’est d’abord un mode de vie, un ami, un credo, une espèce de culte. »
« Et une sorte de poésie, » dit Carabella.
Sleet hocha la tête. « Oui, ça aussi. Et une mathématique. Il enseigne le calme, le contrôle, l’équilibre, le sens du placement des choses et la structure sous-jacente du mouvement. Il y a une musique silencieuse. Il y a surtout la discipline. Ai-je l’air prétentieux ? »
Le petit homme Sleet dans le fantasme de Silverberg qui décrit avec tant d’éloquence les nombreux visages de la jonglerie est membre d’une troupe de jongleurs sur une planète très lointaine, plusieurs siècles dans le futur. Nous discuterons de quelques-unes des nombreuses dimensions de la jonglerie sur notre minuscule planète Terre du point de vue de Darwin (Quelle est l’origine de l’espèce jongleur ?), Newton (Quelles sont les équations du mouvement ?), Faraday (Comment peut-il être mesuré ?) et Edison (L’inventivité américaine peut-elle faciliter les choses ?). Mais nous essaierons de ne pas oublier la poésie, la comédie et la musique de jonglerie pour le futur et le présent de Carabellas et Margaritas. Cela vous semble-t-il prétentieux ?
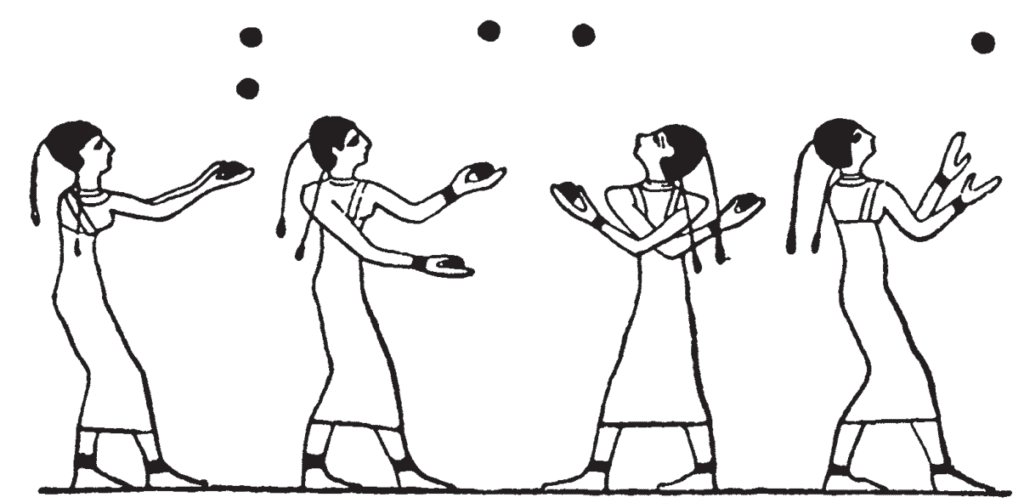
Sur la planète Terre, le jonglage a commencé il y a plusieurs siècles et dans de nombreuses civilisations différentes et lointaines. Une fresque sur la tombe égyptienne de Beni Hassan datant de 1900 avant JC montre quatre femmes jonglant chacune avec trois balles (Fig. 1). La jonglerie s’est également développée de manière indépendante très tôt en Inde, en Orient et dans les Amériques parmi les cultures indiennes et aztèques.
L’île de la mer du Sud de Tonga a une longue histoire de jonglerie. George Forster, un scientifique de l’un des voyages du capitaine Cook, a écrit :
Cette fille, vive et agile dans toutes ses actions, jouait avec cinq gourdes, de la grosseur de petites pommes, parfaitement globulaire. Elle les jeta continuellement en l’air l’une après l’autre, et ne manquait jamais de les rattraper avec une grande dextérité, au moins pendant un quart d’heure.
Le premier historien grec Xénophon, vers 400 av. J.-C., décrit dans Le Banquet l’incident suivant.
A cette occasion, l’autre fille a commencé à accompagner la danseuse à la flûte, à ses côté un garçon lui apportait les anneaux jusqu’à ce atteindre le nombre de douze. Elle les a pris et, tout en dansant, les a lancés en tourbillonnant dans les airs, en dosant les lancer à la bonne hauteur afin de les rattraper à un rythme régulier. Sous le regard de Socrate, il remarqua : « L’exploit de cette fille, messieurs, n’est qu’une des nombreuses preuves que la nature de la femme n’est vraiment pas inférieure à celle de l’homme, sauf dans son manque de jugement et de force physique. »
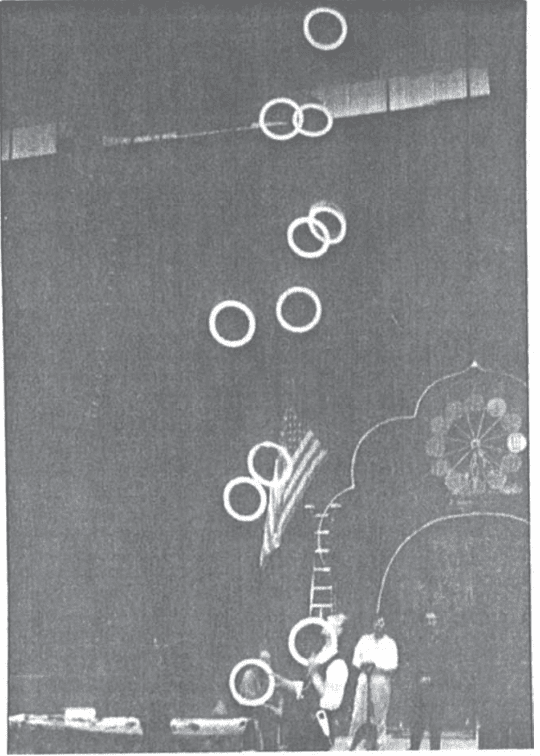
Cet extrait est intéressant à plusieurs niveaux. Au niveau du jongleur, la fille a-t-elle jonglé avec douze anneaux à la fois ? Il s’agit d’un exploit stupéfiant – au cours des vingt-trois siècles écoulés depuis lors, personne n’a atteint ce record, le plus élevé étant le grand jongleur russe, Sergueï Ignatov, qui en fait neuf régulièrement et parfois onze dans son numéro (Fig. 2). Cependant, qui pourrait demander de meilleurs témoins que le grand philosophe Socrate et le célèbre historien Xénophon ? Ils savait sûrement tous les deux compter jusqu’à douze et étaient des observateurs attentifs.
A un autre niveau, il est amusant de constater comment Socrate, s’éloigne de sa fameuse méthode d’enseignement par les questions, en faisant ce constat définitif, il souffre immédiatement de la fièvre aphteuse. S’il avait placé ses neuf mots avant la fin, il aurait pu être le prophète prémonitoire du mouvement pour l’égalité des femmes.
À l’époque médiévale, les bouffons de la cour et les troupes de ménestrels itinérants combinaient souvent les trois arts de la jonglerie, de la magie et de la comédie. Une « rue des prestidigitateurs», où des spectacles quotidiens pouvaient être vus, était une caractéristique de nombreuses villes. Au début du siècle actuel, le vaudeville, les cirques et le burlesque étaient une frayère pour les jongleurs. De nombreux jongleurs de cette période ont combiné une comédie avec leur jonglage et certains des grands comédiens, Fred Allen (présenté comme le pire jongleur du monde), Jimmy Savo (Je jongle avec tout, de la plume au piano !) et WC Fields (comédien distingué et plus grand jongleur sur terre, clochard excentrique) ont évolués à partir de ce contexte.
Les jongleurs sont certainement parmi les plus vulnérables de tous les artistes. Les musiciens et les acteurs peuvent généralement couvrir leurs pirouettes, mais si un jongleur fait une erreur, « c’est d’une beauté ! » Cela a conduit à travers les siècles à un grand nombre de répliques comiques et de fourberie pour la prise manquée ou la massue oublié. Les livres sur la jonglerie contiennent des sections entières sur la façon de se sauver la face dans de telles situations. La Dent a présenté la « la Salle de Serment », une partie de la scène audacieusement décorée et dissimulée dans laquelle il se retirerait s’il manquait un tour. D’autres portent de nombreuses médailles qu’ils enlèvent s’ils font tomber. Un écrivain suggère une grande paire de lunettes à enfiler après une chute. Il y a des dizaines de répliques comiques à utiliser après une erreur, par exemple : « ça fait partie de l’acte, les gars – la partie que je n’ai pas répétée. » WC Fields était apparemment un maître des lancers sauvages, des balles lâchées et d’incroyables récupérations. Les jongleurs experts ne pouvaient pas distinguer les mouvements intentionnels de Fields des échecs réels.
Cette vulnérabilité même peut avoir conduit à la dichotomie entre la comédie et les jongleurs techniques. Les techniciens visent la perfection, s’efforçant de maintenir de plus en plus d’objets en l’air à la fois, le « jeu des nombres » dans le langage de la jonglerie. Albert Lucas, tenant le score de sa propre performance, a rapporté »2 ratés en 46 000 lancers ». Enrico Rastelli, qui aurait jonglé avec dix balles, était le meilleur parmi les interprètes dans ce domaine. Il pouvait faire le poirier à un bras tout en jonglant avec trois balles dans l’autre main et en faisant tourner un cylindre sur ses pieds.
Il y a eu de nombreuses jongleuses talentueuses. Nous avons déjà mentionné cette dame grecque qui était peut-être la championne des nombres de tous les temps. D’autres dont Lottie Brunn (Fig. 3), la seule femme à se produire en solo dans le ring central des Ringling Brothers, et l’enfant star Trixie d’Allemagne. Une photographie du livre Will Mariner de Somerville montre une femme aux Tonga en train de doucher huit balles – un exploit incroyable (la douche étant un moyen très difficile de garder de nombreuses balles en l’air).
Avec l’avènement des différents médias électroniques (radio, cinéma et télévision), le vaudeville et les cirques sont condamnés et la jonglerie décline. Cela a duré plusieurs décennies et beaucoup de grands jongleurs ont cherché des pâturages plus verts.
Récemment, cependant, il y a eu un renouveau de cette compétence ancienne, en particulier chez les jeunes d’âge universitaire. L’Université du Colorado, l’Université d’État de Pennsylvanie, le MIT, Wesleyan et de nombreuses autres universités ont des groupes de jonglerie actifs. Le marché du jongleur professionnel est encore petit – certains spectacles sur glace, des spectacles permanent de Las Vegas, le cirque Ringling. Des artistes de rue peuvent être vus dans des endroits tels que Greenwich Village, Harvard Square et San Francisco. Cependant, l’idée maîtresse du jonglage aujourd’hui est qu’il s’agit d’un loisir stimulant pour les amateurs. Cela peut impliquer non pas une seule personne essayant de jongler avec cinq balles, mais deux personnes passant six massues ou plus entre elles, ou, en fait, vingt personnes dans un schéma très complexe de passes de massue.
La jonglerie semble plaire aux personnes douées pour les mathématiques – de nombreux jongleurs amateurs sont des programmeurs informatiques, des majors en mathématiques ou en physique, etc. Un jongleur averti, lui même professeur de mathématiques, a déclaré à un journaliste que quarante pour cent des jongleurs sont « enclins aux algorithmes ». Dans l’article du New York Times, il est apparu que « quarante pour cent ont une tendance logarithmique. » (Ce curieux anagramme a probablement mieux transmis le sens que l’original à la plupart des lecteurs.) Malgré cet appel à l’esprit technique, il semble y avoir très peu de littérature mathématique ou scientifique concernant la jonglerie.
La jonglerie semble également être une compétence que les très jeunes peuvent bien maîtriser. WC Fields était un bon jongleur à quatorze ans. Albert Lucas, l’un des meilleurs artistes au monde, a grandi dans une famille de cirque et aurait jonglé cinq balles à l’âge de cinq ans. Il a maintenant dix-neuf ans et a joué plusieurs années avec les Ice Capades (Fig. 4). (Notez non seulement les neuf anneaux mais l’embout buccal et la balle et l’anneau sur une jambe.) D’autres jeunes interprètes sont Demetrius et Maria Alcarese, qui, dans leur adolescence, montrent d’excellent potentiel. Dans les différentes compétitions de 1980 de l’Association internationale des jongleurs, les épreuves juniors (moins de trois ans d’expérience), seniors, sept balles, cinq massues et équipes ont toutes été remportées par des adolescents ou au début de la vingtaine. Barrett Felker et Peter Davison ont été particulièrement impressionnants qui, avec Keziah Tannenbaum, ont remporté l’épreuve par équipe et se sont affrontés entre eux en jonglage à cinq massues. Il semble plausible que la capacité de jongler puisse donner des enfants prodiges au même titre que la musique (Mozart, Mendelssohn et Menuhin), les mathématiques (Pascal, Gauss, Abel) et les échecs (Morphy, Capablanca, Reshevsky, Fischer). De plus, il semble probable que l’âge d’aptitude maximale pour la jonglerie soit assez jeune, comme c’est le cas pour des sports comme la gymnastique et la natation.
Les outils des jongleurs
Il est bien connu que les sorcières utilisent trois outils de base dans leur métier : la cloche, le livre et la bougie. Les jongleurs, que beaucoup pensent être de proches cousins des sorcières, utilisent également trois outils de base : la balle, l’anneau et la massue.
Les balles sont les plus faciles à apprendre, et les balles de crosse pesant environ cinq onces et deux pouces et demi de diamètre sont très populaires parmi les jongleurs. Cependant, toutes les tailles de balles ont été utilisées, des fèves à la gelée aux ballons de basket. Récemment, un record a été établi en jonglant avec trois boules de bowling de onze livres pour 37 catchs. À l’autre bout de l’échelle des poids, le jongleur mexicain Picasso a jonglé jusqu’à cinq balles de ping-pong en les faisant sortir de sa bouche.
La plupart des jongleurs professionnels aiment les anneaux. Si le jongleur se tient à angle droit par rapport au public, les anneaux présentent une large zone de visibilité et sont facilement repérable, comme sur la figure 2. De plus, lorsqu’ils sont lancés, la zone présentée au jongleur est inférieure à la moitié de celle des balles, ce qui entraîne moins d’interférences. Cela conduit probablement à des nombres plus élevés en jonglerie avec anneaux qu’en jonglerie avec balle.
Bien que les balles et les anneaux soit anciens, il semble que les massues ne datent que de la fin du 19ème siècle. A cette époque, l’art de balancer les « massues indiennes » est devenu populaire. C’est une forme d’art élégante et exigeante en soi. Il appartenait cependant aux jongleurs de découvrir les possibilités de lancer des massues et, plus excitant encore, de les échanger avec des partenaires. La vue de deux personnes avec six massues tournant rapidement était électrisante. Les premières massues ont été tournés à partir de bois massif et étaient assez lourds. Les massues modernes sont en plastique, souvent avec un axe en bois au milieu, ou en fibre de verre. Ils pèsent beaucoup moins que ceux en bois, environ neuf onces et mesurent environ dix-neuf pouces de long.
Nous avons parlé plus tôt des outils de base des sorcières, cloche, livre et bougie. Leur instrumentation secondaire devrait inclure un chaudron, un manche à balai et les entrailles d’un crapaud. Si ceux-ci semblent un peu exotiques, pensez aux objets que les jongleurs utilisent.
Les jongleurs jongleront avec presque n’importe quoi : foulards, ustensiles de cuisine, assiettes chinoises, raquettes de badminton et torches enflammées. Un jongleur à trois balles utilise un poulet en caoutchouc, une tête de laitue et un bonbon M&M. Le choix d’armes ultime est probablement celui des Flying Karamazov Brothers, un groupe d’interprètes totalement fou, fou même selon les normes des jongleurs. Ils annoncent qu’ils vont jongler avec une tronçonneuse et sortir une tronçonneuse jouet totalement inoffensive. Cependant, ils suivent avec une vraie machine fonctionnant à pleine vitesse et la balancent.
Les assiettes chinoises et les foulards fins impliquent l’aérodynamique – l’interaction de l’objet en vol avec l’air. Les objets de jonglage les plus courants, anneaux, balles et massues, sont suffisamment massifs par rapport à leur surface, et leurs vitesses suffisamment lentes, pour que de tels effets puissent être ignorés.
A l’instant où un objet de jonglerie quitte le contact avec la main du jongleur, il entre dans le monde de la dynamique analytique, libre du contrôle du jongleur mais soumis aux lois et théorèmes de Newton, Euler, Poinsot et Poincaré. Il semble peu probable que l’un de ces mathématiciens ait jamais fait une cascade à trois boules, mais leurs équations différentielles décrivent non seulement le mouvement complexe des planètes et des satellites, mais aussi les »polhodes », »herpholodes » et »lignes invariables » d’une massue de jonglerie en mouvement.
Que pouvons-nous apprendre des principes mécaniques sur le mouvement d’une massue ? Tout d’abord, et le plus simple, son centre de gravité suivra une trajectoire parabolique. La relation entre la hauteur et le temps sera donnée par A = « 4 gr », où A est mesuré à partir du sommet de la trajectoire et g = 32ft/seconde est l’accélération de la gravité. Par exemple, si un jongleur lance une balle à deux pieds en l’air et l’attrape avec sa main au même niveau, à deux pieds au-dessous de son point le plus haut, le temps de vol serait de 2V2h/g ou 0,7 seconde. La distance horizontale parcourue n’a pas d’importance.
Il faudra exactement le même temps pour monter et descendre directement ou à l’aide d’un partenaire, disons à six pieds de distance, tant que le déplacement verticale est le même.
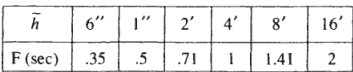
Si l’objet est envoyé à une hauteur H1, et attrapé après une chute de H2, le temps de vol serait donné par √(2H1/g) +√(2H2/g). Dans la plupart des cas de jonglerie, H1 et H2 sont assez proches, la formule approximative 2√(2H/g) peut être utilisée, où H est la moyenne des deux distances. Le tableau suivant montre le temps de vol F pour diverses valeurs de H allant de six pouces (une cascade rapide à trois billes) aux seize pieds que nous estimons pour les onze anneaux d’Ignatov sur la figure 2.
Beaucoup plus complexe que le mouvement du centre de gravité est le mouvement de rotation d’un objet en vol libre. C’est un sujet qui a été largement étudié par de nombreux mathématiciens aux XVIIIe et XIXe siècles. Le mouvement dépendra de la distribution des masses du corps, qui peut se résumer à son ellipsoïde d’inertie. Il est à noter que les trois objets de jonglerie préférés sont très particuliers en ce qui concerne leurs ellipsoïdes d’inertie. La balle a trois axes d’inertie égaux, l’anneau en a deux égaux et l’autre très petit, et la massue en possède deux égaux et le troisième très grand. Ces trois situations particulières conduisent à un comportement beaucoup plus prévisible que celui d’un objet à trois axes inégaux. Dans ce dernier cas, l’objet montrera une stabilité en rotation autour des axes les plus grands et les plus petits mais pas autour de l’axe intermédiaire. Il est facile et intéressant d’observer cette propriété. Mettez un élastique autour d’un livre pour qu’il ne puisse pas s’ouvrir. Maintenant, lancez-le, avec un tour, de chacune des trois manières possibles. Le livre tournera de manière stable autour de sa dimension la plus courte et de sa dimension la plus longue, mais lorsqu’il tournera autour de la dimension intermédiaire continuera à tourner presque complètement de la manière la plus erratique.
Paternes basiques de jonglerie
« Le rythme croisé du 3 contre 2 est l’un des plus séduisants connus. » Ainsi écrivait Gene Krupa, le grand batteur de jazz, il y a une quarantaine d’années. Il est séduisant, qu’il s’agisse de l’Etude en fa mineur de Chopin ou du propre chœur de tam-tam de Krupa dans »Sing-Sing-Sing » avec son emphase toujours changeante.
L’analogue visuel du rythme à trois contre deux se trouve dans les trois balles du jongleur à deux mains, la cascade à trois balles. C’est le premier schéma que la plupart des gens apprennent et le plus fondamental, et il est capable d’autant de changements que le son d’une cloche.
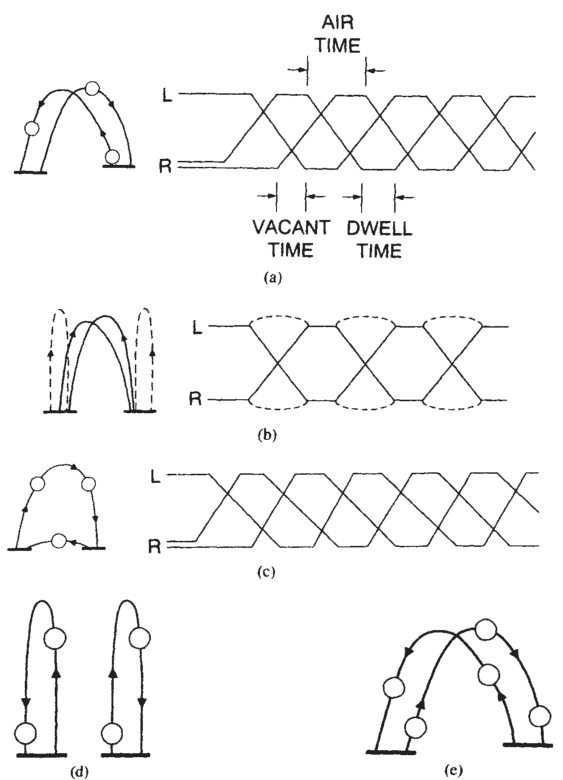
La figure 5a montre comment la cascade à trois balles la plus simple apparaît à un spectateur. Les jongleurs peuvent varier la hauteur du lancer, écarter les mains et même inverser le sens du mouvement. Ils peuvent effectuer des lancers sous les jambes, des rebonds au sol, des lancers dans le dos, des prises par le dessus (pattes de chat), des «chops» et de nombreuses autres variantes.
Le trois contre deux peut se faire avec des massues, des anneaux et, en fait, presque n’importe quoi. Les frères Karamazov dans leur acte offrent au public un choix de trois parmi un assortiment extrêmement varié de possibilités ; des choses comme des tuyaux, des ballons de basket, des massues, des bonbons, etc. Le public par leurs applaudissements en choisit trois et le « plus grand jongleur du monde » tente de les maintenir en l’air. S’il échoue, il reçoit une tarte au visage.
De nombreux jongleurs experts limitent leurs numéros aux variations à trois balles et des livres entiers ont été écrits sur ce sujet. Lors de la convention des jongleurs de 1980, il y avait dix-sept entrées dans la compétition des seniors – chaque participant avait six minutes pour un numéro sans restriction, jugé par sept experts et vu par un public sophistiqué de plusieurs centaines de ses pairs. Les numéros étaient tous bons et allaient de monologues comiques à des expositions hautement techniques.
Le premier prix, cependant, est allé à un jeune homme, Michael Kass, qui n’a utilisé aucun accessoire autre que les trois massues avec lesquelles il jonglait lorsqu’il est monté sur scène. Sa routine était constitué presque entièrement à des variations sur la cascade à trois balles. Les massues étaient doubles, lancées derrière son dos, sous ses jambes, pattes de chat, des flats et d’autres variations sur la musique de Synergy « Synthesizer ». Son étonnant apogée est venu avec une série de »foot-drops » où les massues tombèrent à ses pieds et rattrapait la cascade d’un coup de cheville. Le public a été hypnotisé et lui a fait une standing ovation.
Alors que les variations à trois balles peuvent être totalement fascinantes, le répertoire de jonglage a développé une vaste série d’autres modèles. Un petit échantillon de ceux-ci est montré dans la Fig. 5. Les parties droites de ces diagrammes montrent comment les objets jonglés progresse d’une main à l’autre avec le temps. L’exemple presque trivial de deux balles et deux mains (Fig. Sb) est inclus en raison de son importance théorique. C’est le cas le plus simple où un choix peut être fait à chaque lancer ; s’il faut échanger les balles ou les garder dans les mêmes mains.
La douche à trois balles (Fig. 5c) est similaire à la cascade à trois balles mais avec un timing différent ; le lancer de gauche à droite allant presque horizontalement de sorte que l’ensemble du motif ressemble davantage à des balles tournant en cercle.
Quatre balles sont généralement faites de l’une des deux manières suivantes : la »fontaine » (Fig. Sd) où les deux mains ne sont pas synchronisées et qui, en fait, équivaut à deux balles dans chacune des deux mains qui ne s’échangent jamais, ou un mouvement synchrone où les balles peuvent être interverties ou non à chaque lancer.
La figure 5e montre le schéma d’une cascade normale à cinq balles, une généralisation naturelle de la cascade à trois balles. Dans un lancé multiplex, deux balles ou plus peuvent être attrapées dans une main en même temps. Lors des compétitions de 1979, l’un des concurrents a soulevé une exaltation considérable en jonglant avec sept balles avec le système multiplex. Le jonglage multiplex en soi est un art intéressant et pittoresque mais considérablement plus facile que la forme standard où une seule balle entre en contact avec une main à la fois. Après quelques introspections, l’IJA a décidé d’interdire le jonglage multiplex dans ses compétitions de numéros.
La jonglerie uniforme
Nous définirons un mouvement uniforme, c’est à dire des passes sans multiplexage et avec tous les temps d’arrêt identiques (D), tous les temps de vol les mêmes (F) et tous les temps libres les mêmes (V). Les mouvements uniformes comprennent bon nombre des modèles de jonglerie les plus courants, les cascades à trois, cinq et sept balles, deux ou trois dans une main, la fontaine à quatre balles et de nombreuses routines de passes entre deux jongleurs ou plus. Lors d’une récente convention de jonglerie avec peut-être une centaine de jongleurs au sol, il est apparu que 75 % ou plus travaillaient sur des mouvements uniformes.
Les mouvements uniformes ont une bonne raison de leur popularité ; toutes les mains font à peu près la même chose : elles lancent des balles à la même hauteur, les tiennent pendant le même temps et sont vacantes pendant le même temps.
Le même mouvement uniforme, par exemple la cascade à trois balles, peut bien entendu se présenter sous une multitude de formes. Le jongleur peut jongler au-dessus de la tête (en magicien), il peut lancer les balles sous ses jambes ou derrière son dos ou croiser les bras d’une manière déconcertante. Pour nos besoins, nous ne nous intéressons qu’à l’uniformité des paramètres temporels D, V et F.
Se concentrer sur la jonglerie uniforme s’apparente un peu au géomètre qui passe beaucoup de temps avec des cercles et des triangles. Il est bien conscient de l’existence d’autres formes géométriques, mais la structure simple de celles-ci conduit à d’élégants théorèmes mathématiques. Nous donnerons plus loin quelques résultats relatifs à la généralisation à d’autres types de jonglerie.
Bien sûr, un mouvement peut n’être uniforme que pendant un certain temps. En fait, de nombreuses routines de jongleries sont constituées de segments, qui sont uniformes dans notre sens, avec des mouvements de transition. Les théorèmes qui suivent à propos des jongles uniformes exigent seulement que l’uniformité dure le temps qu’il faudrait une balle pour visiter toutes les mains (s’il les faisait toutes en séquence, c’est-à-dire H(D+F)). Ces théorèmes seront d’abord énoncés et discutés, et plus tard prouvés dans un argument général.
Théorème 1. Dans des mouvements de jonglerie uniforme avec le temps de repos D (dwell), le temps vide V, le temps de vol F, alors où B est le nombre de balles et H le nombre de mains.
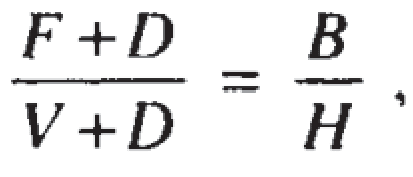
Dans un sens, ce théorème semble presque trivial. Il indique une proportionnalité entre le nombre de balles et de mains, et le temps total pour chaque schéma de balle (F + D) et chaque chemin de mains. Il est cependant plus subtil qu’il n’y paraît, sa preuve dépendant de l’uniformité du jonglage pour au moins H lancers.
Le théorème 1 permet de calculer la gamme des périodes possibles (temps entre les lancers de main) pour un type donné de jongle uniforme et un temps de vol donné. Un jongleur peut modifier cette période, tout en gardant la hauteur de ses lancers fixe, en augmentant le temps de pause (pour augmenter la période) ou en réduisant le temps de pause pour réduire la période. La portée mathématique totale disponible pour un temps de vol donné peut être obtenue en réglant D = O pour la portée maximale et V = O pour la portée maximale dans le théorème 1. Le rapport de ces deux extrêmes est indépendant du temps de vol et ne dépend que du nombre de balles et de mains.
Corollaire . Dans une jonglerie uniforme avec un temps de vol fixe, la plage de périodes possibles est B/(B -H).
Par exemple, dans la cascade à trois balles, un rapport de période 3/1 (ou de fréquence) est possible ; avec cinq balles, le rapport maximum est de 5 à 3. Avec un plus grand nombre de balles, il y a beaucoup moins de portée disponible. À neuf, il est de 9 à 7. Bien sûr, en jonglage réel, la plage possible sera considérablement plus petite que ces chiffres ; il n’est pas possible d’avoir un temps de pause nul ou un temps d’inoccupation nul.
Théorème 2. Si B et H sont relativement premiers (n’ont pas de diviseur commun) alors il y a essentiellement (c’est-à-dire, exception faite d’un labeling) un mouvement jonglé uniforme unique. Les balles peuvent être numérotées de 0 à B -1 et les mains de 0 à H-1 de telle sorte que chaque balle progresse dans les mains en séquence cyclique et que chaque main attrape les balles en séquence cyclique.
Théorème 3 . Si B et H ne sont pas relativement premiers, soit le plus grand commun diviseur avec B = np et H = nq (p et q relativement premiers). Il existe alors autant de types de jongles que de manières de partitionner n en une somme d’entiers.
Par exemple, si m était 5, une partition en 2+2+1 correspondrait à trois jongles disjoints. Il n’y aurait aucun échange de balles possible entre ces trois jongleurs. Chaque « 2 » dans cette partition correspondrait à 27 balles circulant entre 24 mains d’une manière similaire aux cas décrits ci-dessus, sauf qu’à chaque lancer il y a un choix de deux possibilités. Le « 1 » dans cette partition serait une jonglerie cyclique du type du théorème 2, avec p boules circulant autour de q mains sans autre choix.
Dans le cas courant de deux jongleurs, chacun avec trois balles (ou massues), on a B = 6 et H = 4. Le plus grand diviseur commun est 2, qui peut s’écrire comme une somme d’entiers positifs de deux manières : 2 ou 1+1. Le cas de 2 correspond aux jongleurs partant simultanément. Ainsi à chaque lancer il y a le choix entre deux possibilités : un lancer sur soi ou un lancer vers un partenaire. Dans le jonglage en groupe, d’ailleurs, un temps fort analogue à celui d’un chef d’orchestre est utilisé pour assurer le synchronisme.
L’autre partition, 1 + 1, correspond à deux jongleurs désynchronisés. Il n’y a aucun moyen de passer des massues d’une paire de mains à l’autre sans violer la condition de jonglerie uniforme.
Le nombre de partitions de n dans une somme augmente rapidement avec 1 comme le montre le tableau suivant :

Démontrons maintenant ces théorèmes.
Supposons qu’au temps 0, une jonglerie uniforme commence par le lancer d’une balle. Suivons cette balle pendant une période de H catch (au temps H(F +D)). Puisqu’il n’y a que des H mains et la balle a visité H +1 (en comptant celui avec lequel il a commencé) il doit avoir visité deux fois la même main. C’est ce qu’on appelle parfois le principe du pigeonnier en mathématiques ; si vous avez n + 1 lettres dans n pigeonnier, il doit y avoir un pigeonnier avec au moins deux lettres. Le principe du pigeonnier, ou Schubfachprinzip, comme l’appellent les auteurs allemands, ne s’applique qu’aux nombres finis. La théorie de la jonglerie transfinie, comme le cas du Rat Géant de Sumatra, est une histoire à laquelle le monde n’est pas encore préparé.
En se concentrant maintenant sur la main qui a été visitée deux fois par une balle, supposons que le nombre d’attrapés de la balle soit a. Alors le temps entre ces captures était a(D + F). Pendant ce temps, la main, pour satisfaire la condition de jonglerie uniforme, a fait un certain nombre entier, disons b, attrape en même temps, et par conséquent b(D+V) = a(D+F), ou (D+F)/ (D+V) = b/a, un nombre rationnel. En d’autres termes, les temps liés aux balles, F + D, doivent s’aligner exactement avec les temps liés aux mains, D + V, après un nombre entier de lancers.
Soit a/b réduit à ses termes les plus bas, disons p/q. Ainsi p et g seraient le plus petit nombre de captures manuelles et de temps de vol qui pourraient être attribué à la coïncidence.
Considérons maintenant l’ensemble de toutes les balles, disons d1, lancées à l’instant t0. Ceux-ci peuvent être appelés un ensemble synchrone ; avec une jonglerie uniforme, ils seront tous attrapés en même temps et lancés en même temps tant que la jonglerie reste uniforme. De plus, aucune autre balle ne peut tomber dans ce schéma de temps dans la condition d’uniformité. Considérons maintenant le sous-ensemble de balles attrapées par les mains qui ont attrapé ce groupe synchrone à un intervalle de temps (D + V) après le temps t0, c’est-à-dire les prochaines captures de ces mains. Ces balles forment également un ensemble synchrone à un moment ultérieur. La même chose peut être dite pour chaque intervalle de prise en main (D +V) jusqu’à ce que nous atteignions p(D +V) à partir du temps t0, la première fois qu’il est possible pour les balles d’origine de revenir dans les mains d’origine. À ce stade, toutes les balles d’origine doivent être retournées dans les mains d’origine, car aucune autre balle n’aurait pu entrer en synchronisme avec celles-ci et toutes sont chronométrées correctement pour ces mains.
Considérons maintenant les balles lancées par le sous-ensemble de mains dont nous avons discuté à l’instant (D + V) après t0 (un lancer après notre temps initial). Ce sous-ensemble doit fondamentalement être parallèle au sous-ensemble que nous venons de décrire ; ces balles vont aux mêmes mains suivantes et après p lancers reviennent en tant que sous-ensemble aux mêmes mains d’origine.
En continuant cet argument, nous obtenons pd1 balles se succédant cycliquement à travers p étapes, d1 balles à la fois.
Si d1 n’a pas épuisé toutes les balles, on effectue le même processus avec les balles suivantes attrapées après le temps t0. Ceux-ci sont, en un sens, totalement disjoints du premier sous-ensemble. Ils ne peuvent pas être attrapés par les mains impliquées dans la première séquence. Par conséquent on obtient un sous-ensemble totalement disjoint des balles jonglées par un sous-ensemble totalement disjoint des mains.
En continuant ainsi, on épuise toutes les balles et toutes les mains. Le nombre total de balles, B, est donc égal à Σpdi ; et le nombre total de mains, H = Σqdi.
Le jonglomètre
« Certains fils de pute vont inventer une machine pour mesurer le printemps avec »
Afin de mesurer les différents temps de séjour, temps libre et temps de vol impliqués dans la jonglerie réelle, une instrumentation a été développée. Le premier de ces appareils utilisait trois chronomètres électromagnétiques, précis à environ 0,01 seconde (10 millisecondes). Ceux-ci ont été activés par un circuit de relais. Les relais étaient reliés à un treillis de cuivre flexible qui était placé sur l’index et l’index de la main du jongleur. Les balles de crosse étaient recouvertes d’une feuille conductrice. Lorsque l’un d’eux a été attrapé, il a fermé la connexion entre les deux doigts, provoquant le démarrage d’une horloge. Les contacts à coupure ont permis la mesure des temps libres, et les contacts à deux mains ont permis la mesure des temps de vol. Les anneaux et les massues de jonglerie ont également été rendus conducteurs avec du papier d’aluminium afin que les différents temps puissent être mesurés.
Alors que ce système était fonctionnel, il nécessitait plusieurs personnes pour observer et enregistrer les observations, et nous l’avons remplacé par une version informatisée utilisant un ordinateur Apple II. Celui-ci utilise essentiellement le même agencement de capteurs, des manchons en cuivre pour les doigts connectés aux « pad » de l’ordinateur. Un programme informatique affiche le temps en millisecondes des différents lancers et reprises.
Les résultats préliminaires des tests de quelques jongleurs indiquent que, avec le jonglage de balles, le temps libre est normalement inférieur au temps de repos, V variant dans nos mesures de cinquante à soixante-dix pour cent de D. Bien sûr, les jongleurs ont une grande liberté pour changer ce rapport, en particulier en jonglant avec un petit nombre de balles.
Avec un jongle à trois mains, une temporisation de 0,27 sec. contre un temps d’inactivité de 0,17 seconde a été mesuré. Avec trois massues, les chiffres typiques étaient de 0,52 seconde d’arrêt, de 0,20 seconde d’inactivité et de 0,56 de temps de vol. Les massues entraînent un plus grand ratio de temps d’arrêt/temps libre en raison de la nécessité d’arrêter la rotation d’un club et de la recommencer. À chaque prise, l’énergie de rotation est entièrement dissipée et doit être fournie à nouveau à chaque lancer. Curieusement, après tout cela, la massue tourne dans le même sens que le jongleur.
Combien pèsent les jongleurs ?
Regarder une compétition de jongleurs travaillant avec des boules de bowling de onze livres m’a récemment rappelé une vieille énigme que je vais reformuler comme suit.
Claude Crumley tombe sur un canyon. Il porte trois battants de cuivre de sa dernière course. Claude pèse 98 kilos et chaque battant 1 kilo. Le pont qui enjambe le canyon peut transporter 100 kilos. Comment Claude peut-il traverser le canyon ?
La réponse voulue est que Claude traverse en faisant une cascade à trois battants. J’espère sûrement qu’il n’essaiera pas ça, car il serait catapulté dans le canyon. Toutes les forces gravitationnelles sur les objets d’un jongleur dans les airs doivent être supportées essentiellement par ses pieds, par le biais des forces plus importantes vers le bas lorsqu’il accélère les objets vers le haut. En d’autres termes, le centre de gravité de l’ensemble du système, jongleur et objets, accélérerait vers le bas si une force moyenne du poids de ce système n’était appliquée vers le haut, et cela ne peut venir que de ses pieds. Dans la figure 2, les pieds d’Ignatov appuient avec une force moyenne de son poids plus celle des onze anneaux, tout aussi sûrement que s’il avait les anneaux autour de son cou, et tout aussi sûrement qu’Isaac Newton était assis sous ce pommier.
Pourquoi la jonglerie devient-elle si difficile si vite ?
La plupart des gens peuvent apprendre à faire 20 ou 30 captures d’une cascade de trois balles en une semaine ou deux, et certains apprennent en quelques heures. Monter à nouveau jusqu’à quatre balles (essentiellement deux dans chaque main) n’est pas extrêmement difficile. Les gens font cela en quelques semaines de pratique. La cascade à cinq balles est en effet une autre affaire. J’ai demandé à de nombreux jongleurs de cinq balles combien de temps il leur a fallu pour apprendre. Les réponses allaient de six mois à deux ans, et il s’agissait de jongleurs talentueux et dévoués. Six balles, trois dans chaque main, c’est encore un pas en avant dans la difficulté, et sept balles est un point que très peu de jongleurs atteignent. Lors de la convention Fargo de 1980, un concours a été organisé pour jongler avec sept objets (balles, anneaux ou massues). Seuls six sont entrés, et le temps le plus long enregistré était de 5,6 secondes, vingt-six captures. Un certain nombre d’autres jongleurs de sept objets sont connus qui n’étaient pas inscrits ou présents à cette convention mais le nombre est très petit, probablement moins de dix. Nous estimons que moins de vingt-cinq personnes aux États-Unis peuvent jongler avec sept objets pour plus de vingt-cinq prises.
En entrant dans la stratosphère, nous arrivons aux superstars de la jonglerie. Parmi ceux-ci se trouve la figure légendaire Enrico Rastelli, qui était célèbre pour de nombreux numéros d’équilibre complexes et aurait jonglé avec dix balles. Il exerça son métier comme les musiciens font le leur, dix heures par jour, et mourut à seulement 35 ans. L’actuel champion du monde du « jeu des nombres » est sans conteste la grande star soviétique du cirque moscovite, Sergueï Ignatov. Il jongle très solidement avec neuf anneaux dans son numéro et peut en faire onze à l’occasion. Un autre prétendant sérieux est l’Américain Albert Lucas, qui a commencé très jeune dans une famille de cirque et jongle maintenant avec dix anneaux. Sur la photo, il a neuf anneaux mais notez aussi l’anneau qui tourne sur sa jambe, la balle en équilibre dans sa bouche et qu’il est en équilibre sur un patin à glace, vraiment un incroyable exploit de jonglerie.
Pourquoi ça devient si dur si vite ?
Pour commencer, supposons qu’un jongleur ait besoin du même temps d’arrêt et du même temps libre, qu’il jongle avec trois ou neuf balles. D’après le théorème 1, en pensant à tous les termes fixés sauf le nombre de balles et le temps de vol, nous voyons que le temps de vol augmente linéairement avec le nombre de balles. Or le temps de vol, comme nous l’avons vu, n’augmente que comme la racine carrée de la hauteur de lancer, qui est proportionnelle à l’énergie. Ainsi, nous sommes déjà confrontés à des besoins en énergie et en hauteur qui augmentent à peu près comme le carré du nombre d’objets jonglés.
Cependant, la situation est bien pire que cela. Il y a beaucoup de retours positifs douloureux au travail. Premièrement, lancer des objets plus haut nécessitera un temps d’arrêt plus long pour accélérer. Deuxièmement, il y a toujours une dispersion dans les angles de lancer. Avec la même dispersion d’angle, la dispersion de l’endroit où les objets atterrissent augmente proportionnellement à la hauteur de projection. Le jongleur aura donc de plus en plus de mal à rattraper et consommera plus de temps. Plus grave encore est la dispersion de la vitesse verticale du lancer. Cela peut provoquer la chute de deux objets, l’un un peu haut et l’autre un peu bas, presque en même temps, ce qui rend impossible de les attraper tous les deux.
Tous ces facteurs doivent réagir les uns sur les autres – la dispersion de l’angle et du temps de vol force un temps d’arrêt et un temps vacant plus longs, ce qui nécessite à son tour des lancers plus importants. Dans les nombres supérieurs, cette boucle vicieuse ne peut être maîtrisé que par le lancer le plus précis en hauteur, en angle et en tempo.
Jonglerie rebondissante
Les choses ne tombent jamais vers le haut, vous savez. C’est un plan de ma propre invention. Vous pouvez l’essayer si vous le souhaitez.
La jonglerie avec rebond est une variété intéressante de jonglage où les balles sont lancées vers le bas et rebondies sur le sol plutôt que lancées vers le haut. Il est possible de faire tous les modèles de jonglerie de base – cascades à trois et cinq balles et autres – de cette manière à l’envers.
Il y a des avantages et des inconvénients à jongler avec ldes rebonds par rapport à la jonglerie aérienne. Premièrement, en jonglant avec rebond, une grande partie de l’énergie dépensée à chaque lancer est conservée. Les balles en caoutchouc hautement compressé ( »super balles ») s’élèveront à 0,85 de la hauteur d’origine. Cela signifie que le jongleur de rebond ne doit fournir que 15 % de l’énergie que le jongleur de lancer le ferait pour une hauteur de lancer donnée. Cela implique aussi probablement moins de dispersion à la fois dans le temps et dans la direction, car celles-ci ont tendance à être proportionnelles aux besoins énergétiques.
Du côté négatif, en jonglant avec rebond, les propres mains du jongleur interfèrent avec sa ligne de mire vers les balles jonglées. De plus, la partie de la trajectoire des balles que nous pensons la plus optimale pour la prédiction, à savoir à mi-chemin entre le lancer et le point de capture, se trouve désormais au sol sous un angle de vision très mauvais. Lors du lancer, les yeux sont dans une bonne position pour voir les sommets des orbites paraboliques.
Tout compte fait, il semble probable que le jonglage avec rebond soit plus facile que le jonglage au lancer, mais très peu de gens se spécialisent dans ce domaine. J’ai vu des jongleurs de rebond travailler cinq balles à moins de deux pieds de leur surface de rebond ; plus vite que ces mêmes jongleurs ne pourraient faire une cascade de lancer de cinq balles.
Il existe d’autres possibilités intéressantes dans le jonglage avec rebond. Si la balle de jonglerie a un coefficient de friction élevé avec le sol (comme le font les »super balles »), lorsqu’elle est lancée à un angle contre le sol, une fraction considérable de la composante horizontale de l’énergie est transformée en énergie de rotation. S’il continue et frappe à nouveau le sol, le deuxième rebond semble être étonnamment plat. Plus intéressant, cependant, est de le laisser heurter le dessous d’une table, Fig. 6. L’énergie de rotation le fait alors revenir de très près sur sa trajectoire d’origine, rebondir à nouveau sur le sol et revenir très près de la main qui l’a lancé. Il est possible de faire rebondir et jongler à plusieurs balles de cette façon sous une table. Puisque chacun fait trois clics forts à chaque lancer, l’effet audible se rapproche de celui d’un roulement de tambour.
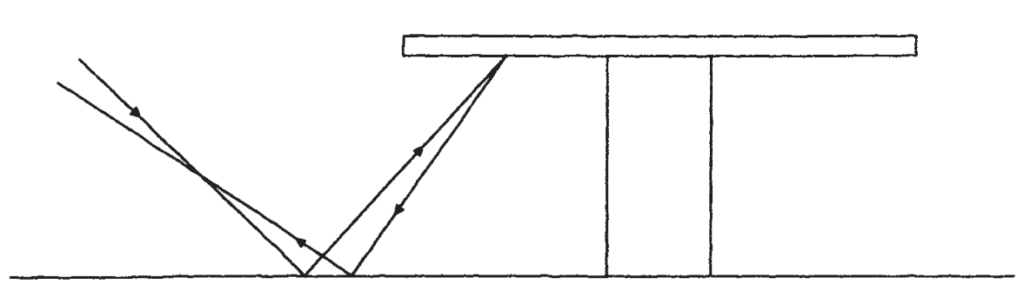
Autrement dit, cette situation est une sorte de boomerang où l’on peut lancer la balle de manière assez arbitraire et elle reviendra au même endroit à une légère chute près. C’est un peu le délice d’un jongleur, sauf que chaque balle revient à la main qui l’a lancée. Pour atteindre l’autre main, comme dans une cascade normale, il faut déplacer l’autre main à l’endroit où se trouvait la main qui lançait.
Une généralisation de cet automatique retour en jonglage rebond qui donne pourtant un échange de mains qui peut être construite comme suit.
Si un rayon lumineux part d’un centre d’une ellipse, il se reflétera dans l’autre centre. Si cette ellipse est tournée autour de son axe principal, nous avons un sphéroïde allongé, et le rayon lumineux d’un centre dans n’importe quelle direction dans l’espace tridimensionnel sera réfléchi vers l’autre centre.
Bien que les balles ne réfléchissent pas exactement comme les rayons lumineux, leur comportement est assez proche. Imaginez une parabole réfléchissante d’environ 20° de long sur environ 18° de large en forme de partie d’un sphéroïde allongé. Les deux centres seraient à environ 4 pouces au-dessus de la surface où se trouvent normalement les mains du jongleur. Il peut lancer une balle n’importe où avec une main tant qu’elle touche l’assiette, et elle reviendra automatiquement dans l’autre main !



