Des glaçons dans mon whisky

Avec un où deux glaçons dans ton whisky ?

Amateurs de Whisky, vous êtes les bienvenus. Non pas que je le suis moi-même (je ne bois que très occasionnellement). Mais autour d’un verre, il est possible de siroter tranquillement un bon whisky 30 ans d’âge tout en discutant correctement de comment ça fonctionne. Et ce qui est bien, c’est qu’on peut faire de l’énergétique de précision à partir de cette boisson spiritueuse.

Naturellement, on nous répète sans cesse que l’abus d’alcool est dangereux pour la santé. J’en appelle donc à votre sens des responsabilités pour ne pas expérimenter plus que nécessaire ce qui se dit sur cette page.

Éventuellement, un petit verre de temps en temps peut participer à agrémenter certaines situations d’une agréable douceur. C’est notamment pour cela qu’au temps du moyen-âge, les seigneurs prirent l’habitude de trinquer leurs verres avant de boire.

Cependant, comme toutes les bonnes choses, en faire une habitude peut devenir une source de problème chronique. Car c’est effectivement dans la rareté que nous puisons ces précieux moments inhabituels sans équivalent. Alors, à votre rythme mesdames et messieurs.

Si je m’intéresse particulièrement au whisky, c’est qu’il y a cette question qui me turlupine depuis quelques temps. Une question pourtant essentielle, celle du rafraîchissement !

Bon, il n’y a peut-être que moi que ça amuse ! Alors consommer avec modération.

Pour un amateur de whisky, le glaçon est d’une importance cruciale. Et là, et bien il y a deux écoles :

Ainsi, on peut voir et largement vérifier les vertus du glaçon, ou préférer les pierres à mettre au congélateur.

Comment comparer l’efficacité des deux procédés ? Rien de plus simple, on calcule, et on compare, mais pour se faire un avis, il faudra bien d’autres arguments.

Quoi étudier

Pour établir une telle comparaison, il faut correctement définir les limites du système que l’on étudie. On ne parlera pas, par exemple de l’ambiance tourbé au coin de cette immense cheminée qui fait ressortir un charme certain dans les lointaines contrés des Highlands.

Nous possédons simplement un verre à whisky dont nous versons une quantité de seulement 4 cl de cette boisson, la dose normative. Étant donné que la bouteille sort de l’étagère, elle est supposée à température ambiante (nous considérerons 20°C).

Pour que nous puissions apprécier à son juste titre ce fameux breuvage, il sera donc nécessaire de diminuer la température. Et donc de rafraîchir le liquide à 14°C. Ainsi, pour simplifier notre problème, nous ne considérerons pas d’échange avec le verre, et nous pouvons utiliser n’importe quel moyen pour rafraichir le spiritueux.

Voici une définition précise du problème à résoudre.

Une différence 6°C, ce n’est pas beaucoup étant donné le volume considéré. Pourtant, à partir de ces hypothèses, on peut se demander quel serait la solution la moins énergivore ? Et donc il faut faire l’exercice de comparaison.

Glacer de l’eau

Pour transformer de l’eau en glace, il faut fournir au volume d’eau considéré une certaine quantité d’énergie pour la refroidir. Elle est exprimée en quantité de chaleur négative, car on y retire de la chaleur. Nous souhaitons donc savoir quelle quantité d’énergie nous apportons à un volume d’eau pour l’emmener à -18°C (valeur courante pour un congélateur).

Admettons que la température de l’eau à la sortie du robinet soit de 15°C. Elle est donc placée dans ce genre de bac à former des cubes de glace, puis ce bac est installé dans le congélateur. Rien de bien compliqué pour le moment.

Pourtant, si on décrit maintenant d’une manière purement physique les différentes étapes qui se produisent, l’eau évolue d’une température de 15°C à -18°C. Or, elle passe forcément par 0°C, et à ce moment-là, il y a ce qu’on appelle dans le jargon technique du thermicien un changement de phase. L’eau qui se situe dans un domaine ou la température est positive, évolue vers un état solide en passant sous la barre du 0°C. On appelle cela, la phase de solidification. Puis une fois congelé, le cube formé continue sa route jusqu’à -18°C.

Dans cette transformation, nous avons donc trois phénomènes à étudier.

Il y a donc, une première quantité d’énergie pour faire chuter la température vers 0°C.

Puis une quantité d’énergie non-négligeable qu’il est nécessaire d’apporter pour que la glace prenne, en quelque sorte l’eau passe de l’état liquide à 0°C à l’état solide toujours à 0°C.

Enfin, il y a à nouveau une phase de chute de température pour refroidir la glace. Au moment du prélèvement, le glaçon sera à la température du congélateur, il passe donc de 0°C à -18°C. Nous avons alors besoin de fournir encore une certaine quantité énergétique.

À quelques approximations près…

Étant donné que la masse volumique de l’eau évolue en fonction de la température, en toute rigueur cet exercice présente quelques arrondis, mais qui restent largement négligeables par rapport à ce que l’on souhaite étudier.

Lorsqu’on procède à l’application numérique, nous obtenons les résultats suivants :

• Q1 (de 15°C à 0°C liquide) =  126 joules
• Q2 (de 0°C liquide à 0°C solide) =  668 joules
• Q3 (de 0°C à -18°C solide) =  74 joules
• Q total = 868 joules

Fondre de la glace, un problème de chaleur latente

Lorsque l’eau change d’état, lorsqu’elle passe de l’état solide à l’état liquide, elle dégage beaucoup d’énergie. Nous l’avons vu précédemment avec l’application numérique. L’ordre de grandeur de la quantité d’énergie à apporter à l’eau est nettement plus important lors de ce changement d’état que lors des deux autres étapes de refroidissements.

Pour faire fondre la glace, le fonctionnement s’inverse. La quantité d’énergie apportée sera donc relâchée intégralement dans notre verre de bourbon soit -868 joules.

Sur un temps long, on peut donc considérer que l’état est à l’équilibre. Et donc, il est aisément possible de déterminer la température finale de notre breuvage à la fin de la fonte du glaçon en résolvant cette équation de la chaleur.

Nous ferons bien sûr une approximation en considérant le système liquide + glace adiabatique (le verre est en quelque sorte ignoré).

Avec 1 glaçon, nous obtenons une température finale de 13,9°C, on remarque que c’est donc suffisant pour atteindre ce que l’on souhaite.

À l’aide de ces données numériques, il est facile de résoudre l’équation différentielle qui en découle pour déterminer le temps qu’il faudra pour atteindre la température souhaitée de 14°C. Pour cela, il faut appliquer le premier principe de la thermodynamique et résoudre l’équation différentielle qui y est associée.

On passera au préalable par une évaluation du coefficient de transfert global de convection naturelle en estimant les nombres caractéristiques de Prandtl de Nusselt et de Rayleigh. Le whisky étant constitué principalement d’éthanol, les applications numériques sont estimées sur cette base.

Nous retrouvons un temps d’environ 1 minute et 34 secondes pour un glaçon constitué d’eau. Oui, c’est aussi précis que ça, et la température se stabilisera normalement vers 13,9°C. Ça tombe bien, c’est juste en dessous de ce que l’on souhaite !

Refroidir par d’autres moyens

Certains commerçants nous vantent les mérites de la pierre pour refroidir des boissons alcoolisées. Voyons cela en appliquant exactement la même démarche que précédemment.

Bien évidemment, il est possible de comparer un nombre indéfini de matériaux, mais concentrons nous sur la pierre stéatite, le granit ou l’acier.

Pour de tels matériaux, il n’y a qu’une seule phase contrairement à l’eau. Cela est dû à la température de changement d’état propre à chacun des matériaux qui se produit à des niveaux très élevés pour ceux-ci.

Le plus délicat est certainement d’obtenir des valeurs correctes pour les caractéristiques physiques de certains matériaux, comme la masse volumique, la capacité thermique…

Ensuite, il faut poser correctement le problème à résoudre, trouver volontairement quelques simplifications. Par exemple, les dispositions géométriques sont similaires d’un modèle à l’autre afin de considérer exactement les mêmes dimensions que dans notre premier cas. Cela afin de comparer ce qui est comparable, soit 2 cm3 pour tout le monde.

Puis, nous procédons de la même manière que précédemment, en résolvant l’équation de la chaleur pour 1, 2, 3 voir 4 glaçons. Car il arrive qu’avec un seul glaçon, on n’atteigne pas ce que l’on cherche. Effectivement, dans certains cas, la température n’est pas atteinte si la masse de matière froide n’est pas suffisante. Alors on augmente simplement le nombre d’éléments. De cette manière, nous déterminons le nombre correct d’élément à intégrer pour atteindre la température voulue.

Ainsi, nous retrouvons les températures suivantes :

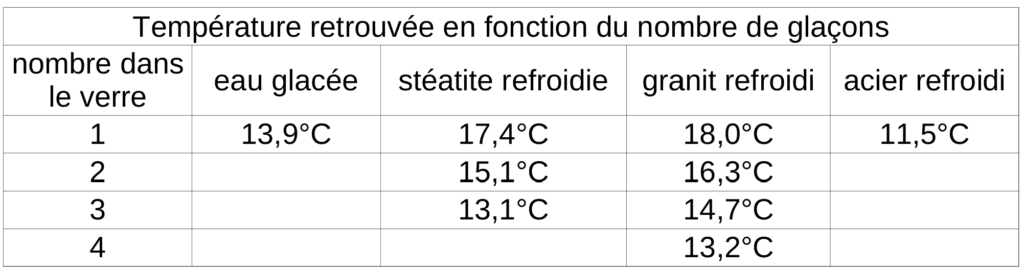
En appliquant la solution de l’équation différentielle, nous retrouvons le temps pour chacun des systèmes et nous pouvons tracer la courbe de refroidissement de chaque système.

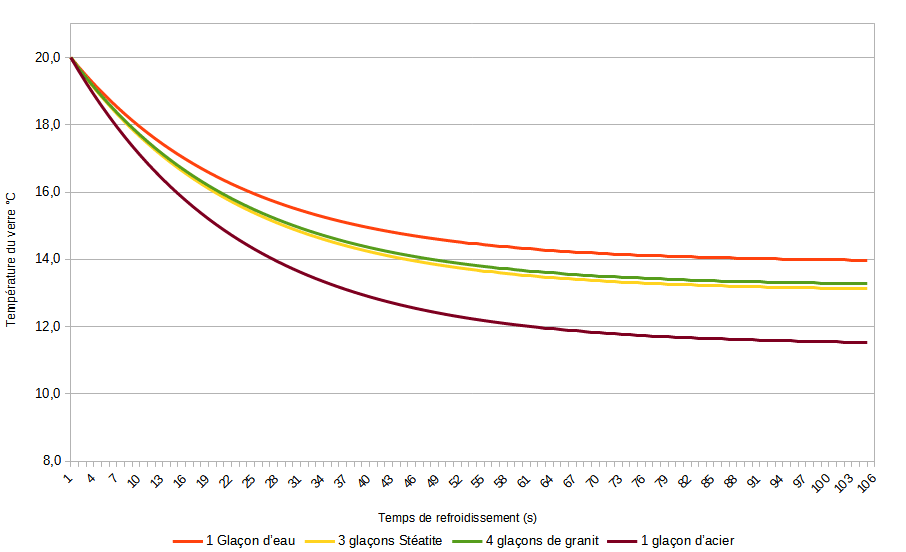
Ainsi, il est possible de déterminer le système adéquat selon les envies.

Il est bien évident qu’en considérant le système whisky+glace totalement adiabatique, certains échanges de chaleur réels ne sont pas visualisables par cette approche sommaire. Par exemple les échanges thermiques avec le verre, avec la pièce ou même avec la main qui porte le verre.

D’une certaine manière, une fois que le glaçon aura libéré toute son énergie (arrivé à la température finale), le système sera réchauffé par l’environnement.

Que faire face à ce genre de problème ?

Tout dépend de ce que l’on veut.

Il est certain que le commerçant qui vous propose ce genre de produit vous donnera toutes sortes d’arguments avantageux pour vous pousser à l’achat compulsif. Seulement, si vous ne savez pas combien en mettre pour assurer le service, cela peut dégrader fortement des conditions optimales de dégustation…

Nous l’avons vu, concernant les autres systèmes que l’eau, tout dépend de la masse volumique et de la capacité calorifique. Ainsi, l’acier présente effectivement d’excellentes propriété à ce niveau. Mais vous le voyez sur le graphique, la température continue de chuter, alors il faut se dépêcher de boire (cul-sec au bout de 26 secondes ! Si c’est la physique qui le dit) .

Au niveau de l’énergie, il est tout à fait possible d’étudier le meilleur système, celui qui demandera moins de joules. Cela étant, ce petit problème de thermique révèle bien d’autres complications que je ne soupçonnais pas au début d’écrire cet article. Je précise que j’ai réalisé une feuille de calcul que je mets à disposition pour les curieux (merci de me contacter).

Vous voyez bien qu’entre la pierre stéatite et le granit, les différences sont très faible, mais il faut quand même un glaçon de plus pour le granit, et donc un coût forcément différent…

Et puis, il y aura forcément un autre paramètre rentrant en jeu dans le bilan de consommation : la taille ou l’efficacité de votre congélateur.

Au niveau du goût, forcément, ça dépend de bien d’autres paramètres qu’un simple bilan énergétique. Et chacun se fera son propre avis sur la question.

Et si vous souhaitez ajuster au mieux le rafraîchissement de votre whisky ou d’une boisson similaire, il est tout à fait possible de passer par d’autres moyens que ce que l’on trouve dans le commerce. En effet, certaines subtilités de notre environnement peuvent être nettement plus appropriées que d’investir dans ce type de pierre à whisky. Mettez directement votre argent là où vous voulez, et obtenez plus de résultats, avec plus de précisions !